有限差分法(陽解法)
偏微分方程式はふつう解析的に解けることは珍しく、ブラック・ショールズの偏微分方程式は稀有な例と考えられる。 コールオプションといってもアメリカ型になるといまだよく知られた演算子で解くことはできない。
ちょっと応用を利かせて新たな偏微分方程式を導いたとしても、一般に公式というようなものは知られていないケースがほとんどであって、 そこから解の式を求められずに行き詰まることは十分ありうる。
したがって解の式は諦めて、なんとか解の値を求めようとするとシミュレーションや近似計算による数値解析を行うことになる。
この項と次の項ではブラック・ショールズ偏微分方程式そのものを使って、数値解析手法を説明しよう。
陽解法の基本
陽解法は境界条件から後退的に数値を求めていくので、オプション価格を求める上ではまことにイメージしやすい。
もともとのブラックショールズの偏微分方程式は、 \[ \frac{\partial C}{\partial t}+rS\frac{\partial C}{\partial S}+\frac{1}{2}\sigma^2S^2\frac{\partial ^2C}{\partial S^2}-rC=0 \] となっているので、これを差分方程式に変換する。差分方程式への変換は次のように行う。
まず満期までの期間$t$を微小単位$dt$でn分割し、$ndt=t$とする。位置を$i=0,\cdots ,n-1$ で表す。
次に株価変化の微小単位を$dS$とし、任意の株価を$S=jdS$で表す。横軸に時間、縦軸に株価をとった平面を考えれば、 $(i,j)$によって離散的な座標(格子点)が生まれる。
オプション価格は時間と株価の関数$C=C(t,S)$であるから、格子点ごとにオプション価格が定まる。
偏微分方程式は独立変数の微小変化と関数の変化との関係を表したものだから、 いくつかの格子点を使えばその格子点間のオプション価格の関係を表すことができるはずである。
このために次のように変化率を離散的に定義する。 \begin{eqnarray*} \frac{\partial C}{\partial t} &= & \frac{C_{i+1,j}-C_{i,j}}{dt} \\ \frac{\partial C}{\partial S} &= & \frac{C_{i+1,j+1}-C_{i+1,j-1}}{2dS} \\ \frac{\partial ^2C}{\partial S^2} &= & \frac{\frac{C_{i+1,j+1}-C_{i+1,j}}{dS}-\frac{C_{i+1,j}-C_{i+1,j-1}}{dS}}{dS} \\ &= & \frac{C_{i+1,j+1}+C_{i+1,j-1}-2C_{i+1,j}}{dS^2} \end{eqnarray*}
$C$の添え字は格子点の位置を表す。現在$(i,j)$にいるとすれば、さらに$S=jdS$、$C=C_{i,j}$として、すべて偏微分方程式に代入する。 \begin{eqnarray*} & & \frac{C_{i+1,j}-C_{i,j}}{dt} + rjdS\frac{C_{i+1,j+1}-C_{i+1,j-1}}{2dS} \\ & & \qquad + \frac{1}{2}\sigma^2(jdS)^2\frac{C_{i+1,j+1}+C_{i+1,j-1}-2C_{i+1,j}}{dS^2} -rC_{i,j}=0 \end{eqnarray*}
求めたいものは$C_{i,j}$なので、これを左辺として整理する。 \begin{eqnarray*} C_{i,j} &=& \alpha C_{i+1,j+1} + \beta C_{i+1,j} + \gamma C_{i+1,j-1}\\ &\alpha & = \frac{1}{2}\frac{dt}{1+rdt}\left( rj + \sigma^2 j^2 \right)\\ &\beta & = \frac{1}{1+rdt}\left(1- \sigma^2 j^2 dt \right)\\ &\gamma & = \frac{1}{2}\frac{dt}{1+rdt}\left(-rj + \sigma^2 j^2 \right) \end{eqnarray*} として差分方程式に変換できた。ただし解が収束するためには、$\alpha,\beta,\gamma>0$でなければならない。
格子点の位置関係は次のようになっていることがわかるだろう。
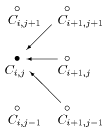
すなわち、先行する3つのオプション価格によって現在のオプション価格が表されることになる。
なぜ先行するオプション価格から後退して現在を表すかといえば、将来の権利行使時点の価格を決めることができるからである。 $j$は理論的には0から無限大だが、適当な株価の幅で定めればよい。
権利行使時点の株価を適当な幅で定めれば、行使価格によっていくつかのオプション価格が定まる。 この明らかに値の定まる(陽解な)終端のオプション価格を利用して、 後退していけば現在のオプション価格が得られるというのが陽解法の原理である。
陽解差分方程式の改善
ブラックショールズの偏微分方程式に対する上記の考え方による適応がつらくなる点は、 $(i,j)$と$(i+1,j)$の格子点において、常に$\frac{\partial C}{\partial S}$と$\frac{\partial ^2C}{\partial S^2}$が等しいと考えることにある。 残念ながら現実はそうではない。
加えて、解を得るために生じる問題は、$\alpha,\beta,\gamma$が負になり、結果として$C_{i,j}$も負になる。 つまり解が収束しない状態が発生しうることである。そしてその原因は$j$の大きさが変化するところにある。
この事態の改善として、熱伝導方程式での解法で行ったと同様に、偏微分方程式の変数変換を行う方法がある。$y=\log S$ とおいて変数変換すると、 \begin{eqnarray*} %\frac{\partial C}{\partial t}&=&\frac{\partial C}{\partial \tau}\frac{\partial \tau}{\partial t}=-\frac{\partial C}{\partial \tau} \\ \frac{\partial C}{\partial S}&=&\frac{\partial C}{\partial y}\frac{\partial y}{\partial S}=\frac{1}{S}\frac{\partial C}{\partial y} \\ \frac{\partial ^2C}{\partial S^2}&=&\frac{\partial }{\partial S}\left( \frac{1}{S}\frac{\partial C}{\partial y} \right)=-\frac{1}{S^2}\frac{\partial C}{\partial y} +\frac{1}{S^2}\frac{\partial ^2C}{\partial y^2} \end{eqnarray*} をもとの式に代入する。
\[ \frac{\partial C}{\partial t} + \left( r-\frac{1}{2}\sigma^2 \right)\frac{\partial C}{\partial y}+\frac{1}{2}\sigma^2\frac{\partial ^2C}{\partial y^2}-rC=0 \]
この段階で目的とする偏微分方程式の係数から$S$が消える。そして上記と同様に差分方程式に変換する。 \begin{eqnarray*} C_{i,j} &=& \alpha^*C_{i+1,j+1} + \beta^*C_{i+1,j} + \gamma^*C_{i+1,j-1}\\ &\alpha^*& = \frac{1}{2}\frac{dt}{1+rdt}\left( \frac{r-\frac{1}{2}\sigma^2}{dy} + \frac{\sigma^2}{dy^2} \right)\\ &\beta^*& = \frac{1}{1+rdt}\left(1- \frac{\sigma^2}{dy^2} dt \right)\\ &\gamma^*& = \frac{1}{2}\frac{dt}{1+rdt}\left(-\frac{r-\frac{1}{2}\sigma^2}{dy} + \frac{\sigma^2}{dy^2} \right) \end{eqnarray*} $\alpha^*,\beta^*,\gamma^*$を一定値とすることができ、最初に正であることを確認すれば解は収束し、 上の差分式のように$j$の増加によって変動することはない。
